By, PhD candidate, Aida Aslanova
Baku Higher Oil School,
Khojaly Avenue 30, Baku, Azerbaijan, AZ 1010
Mobile phone: +994515662320
Contact e-mail: [email protected]
Jalil Jalilov
6 Gulbala Aliyev St, Baku, Azerbaijan, AZ 1010
[email protected]
Abstract
In this research work, the
rheophysical aspects of the non-Newtonian behavior of water during flow in thin
microchannels are considered experimentally. Based on the Bingham model,
rheological parameters of water flow are estimated at different micro-slit
clearances. Using the microchannel model it is established that the nonlinear
rheological effect in the flow of water in micro-slits is mainly caused by the
value of the electrokinetic potential of the system, by controlling which it
is possible to significantly regulate the non-Newtonian nature of the fluid.
1.
Introduction
Currently, the development of low-permeable hydrocarbon reservoirs is becoming
an increasingly urgent task, and therefore, the study of the laws of fluid
movement in sub capillary pores and microcracks is a crucial scientific and
technical problem.
Despite a large number of
experimental and theoretical works, some issues in this area require further research.
According to the results of some experimental
studies, a viscous liquid during flow in low-permeable reservoirs exhibits an
anomalous non-Newtonian character, accompanied by a violation of the linearity
of the filtration process, and, consequently, Darcy's law (1-3, 7-10).
It is
established (4) that starting from a certain critical size of the opening of
the crack, the flow of a Newtonian fluid (water, viscous oil) becomes
non-Newtonian, with the manifestation of an initial pressure gradient and flow
locking.
However, to date, there is no
consensus on the mechanism of these phenomena, although there are different
approaches to explain the abnormal hydrodynamic behavior of liquids during flow
in a low-permeable porous medium and microcracks.
The work (5) is one of the first steps
to study the influence of the electrokinetic potential of the flow on the
hydraulic characteristics of real liquid systems, in which it was revealed that
various thermohydrodynamic effects in heterogeneous liquid systems are largely
determined by the electrokinetic factor, by regulating which it is possible to
significantly change the rheophysical state of the system.
The rheophysical peculiarities of
water flow in the microchannel were considered experimentally.

2.
Materials and Methods
The experimental setup mainly
consisted of a microchannel model, a high-pressure balloon, and a thermostat.
Tap water was used as the working fluid. The microchannel model with a length
of 30cm and a width of 4cm was formed by two parallel smooth steel plates with
a thickness of 1.8 cm. Fig. 1 shows the scheme of the experimental system.

Fig.1. 1-a high-pressure cylinder,
2- A reducer for regulating the supply of compressed air, 3-a container for the
test liquid, 4-a thermal bath, 5-a slot model, 6-a thermostat, 7 standard pressure gauge, 8-thermometers
Microcracks of a given opening (h)
were obtained by installing non-wettable gaskets of the corresponding micron
thickness between the plates. The experiments were carried out at various
values of h in the range of 20÷50 μm.
3.
Results and discussion
Upon reaching a steady flow regime, the flow curves
for water were plotted at different values of the crack opening.
It is
known that the volumetric flow rate of a liquid with a steady laminar flow
between two stationary parallel plates is defined as Q = bh3ΔP/12µL, where, b, L and h, respectively, are the
width, length, and openness of a rectangular slit.
Fig. 2 shows the flow curves obtained from experiments at five values of the opening of the crack h – 20μm, 30μm, 40 μm, 45 μm and 50 μm, at a constant temperature T = 300C.
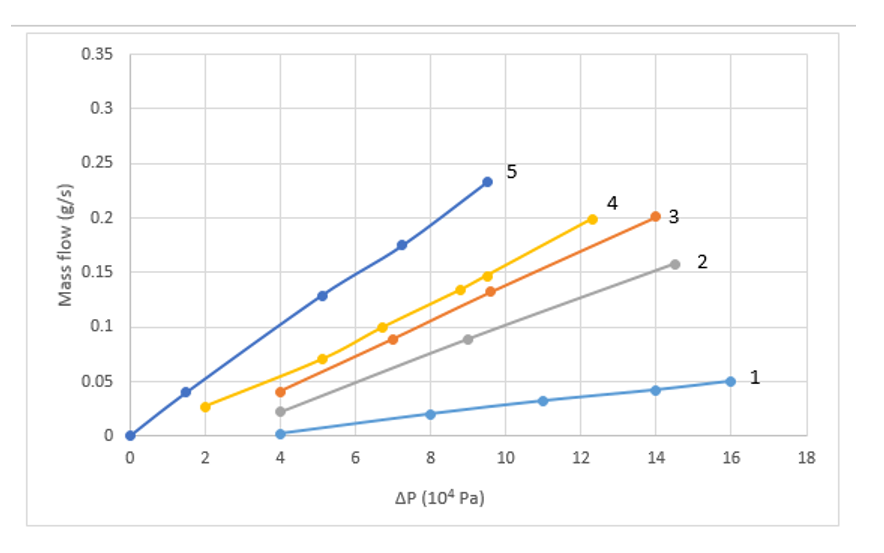
Fig. 2 Flow curves 1 –20 μm, 2 – 30
μm, 3 –40 μm, 4 – 45 μm, 5 – 50 μm
As can be seen, for the crack with
h=30μm, the water flow curve is linear and corresponds to the Newtonian model.
However, at lower values of h, the flow becomes nonlinear – water behaves like
a non-Newtonian fluid with some initial pressure gradient ΔP0 typical
for Bingham fluids, which is consistent with the results of previous studies [4].
With a decrease in the opening of the crack, starting from the threshold value
h = 45 μm, the nonlinear nature of the water increases, and the effect of locking
the flow is manifested, which is maximally expressed at the lowest value of the
gap (h =20μm) in the considered range.
In the
observed transformation of a Newtonian system into a non-Newtonian one,
strengthening of rheological nonlinearity, enhancing of hydraulic resistance in
thin slits, the role of the electrokinetic factor, in particular, the stream
potential, is unconditional. According to Coehn rule (6), a double electric layer
(DEL) is formed at the contact boundary between liquid and solid surface with a
certain electrokinetic potential. The distribution of DEL is rather blurry and the
thickness of the diffusion layer might be several microns. The electrostatic field
created by the DEL affects the character of the flow around the boundary zone.
For channels with sufficiently large opening thicknesses, this effect can be
insignificant. However, for microchannels, the situation becomes principally
different – electrokinetic potential creates additional hydraulic resistance.
In the
experiments, the streaming potential Δφ was measured with a microvoltmeter (CHY
20 Multimeter) using platinum electrodes at the input and output of the model.
The measurement error did not exceed 0.8%.
When
plotting the flow curves, for each individual case, measurements of the streaming
potential Δφ were simultaneously carried out. The values of Δφ, with a pressure
difference of ΔР = 1atm, for different values of the crack opening h,
are shown in Fig. 3. Through the recording of the potential differences between the inlet and outlet of the model, the pressure difference has been kept as 1 atm.
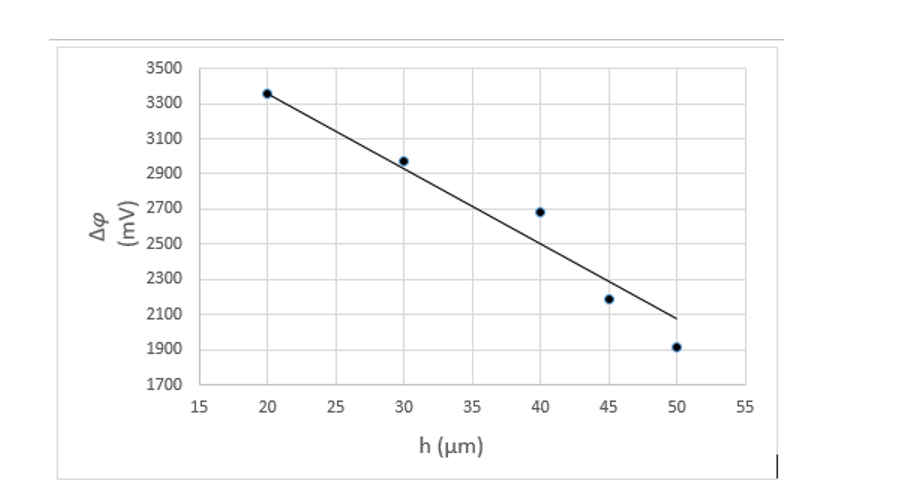
Fig.3.
The dependence of the stream potential Δφ on the magnitude of the
opening of the crack (h).
It is
established that the value of Δφ significantly depends on the opening h and
increases with decreasing of the gap. So, for values of h - 50μm, 45μm, 40μm, 30μm and 20μm, at ΔP=1atm, the average values of Δφ, respectively, are equal to 1910mV,
2190mV, 2680mV, 2975mV, and 3360mV. With a decrease of h, the stream potential
Δφ increases and reaches its highest value at the smallest thickness. (Fig.3).
The
obtained results indicate that the hydraulic characteristics of the water flow
in microcracks significantly depend on the degree of electrokinetic factor of
the flow and by its corresponding variation the flow parameters can be
significantly changed.
The authors are grateful
to Professor Fuad Veliyev for setting up the task and discussing of obtained
results.

Conclusion
References
1.
Feng Wenguang, Giaeli Ge. The problem of
non-Darcy flow at low velocity non-fixed single medium, dual medium. Petroleum
exploration and development. - 1985. - № 1.
2. Chen
Yongming, Juan Zhou, Experimental demonstration of the non-Darcy phenomenon
during low-velocity flow through porous media. Journal of Chongqing University
(Natural Science edition). -2000. - № 1.
3. Prada A.,
Civan F. Modification of Darcy’s law for the threshold pressure gradient.
Journal of petroleum science and engineering. -1999. - № 22 (4). - P. 237-240.
4. Mamedova M.A., Gurbanov R.S. Investigation of
the Rheology of Fluids in Fracture and Pore Channels and Determination of Their
Opening. Journal of Engineering Physics and Thermophysics: Volume 88. Issue 4
(2015), Page 815-824)
5. Veliyev F.H. Study of
electrification of hydraulic flows. Thematic collection of scientific papers
AZINEFTEKHIM. Baku, 1984, 110p(in Russian).
6.
Leonard
B.Loeb B., Static Electrification, Springer-Verlag, Berlin, 1958.
7.
B.A. Grigoriev, D.M. Orlov, N.V. Savchenko et al. Investigation of initial
pressure gradients during filtration through low-permeability reservoir rocks.
Vesti gazovoy nauki: Topical issues in the study of reservoir systems of
hydrocarbon deposits. - M.: Gazprom VNIIGAZ, 2013; 1(12):119-125
8. V.A. Baikov, A.V. Kolonskikh, A.K.
Makatrov et al. Nonlinear filtration in low-permeability reservoirs. Bulletin
of OAO NK Rosneft-2013; 31(2):4-7
9. Wu J, Man Y. Low-velocity non-Darcy
percolation characteristics of low permeability reservoir of single-phase
fluid. Journal of Daqing Petroleum Institute. 1999; 82-84.
10. Li, D.Q.
Electrokinetics in Microfluidics; Elsevier; 2004
11. Hanson, P.; Trigg, T.; Rachal, G.; Zamora M. (1990, September).
Investigation of Barite Sag in Weighted Drilling Fluids. SPE paper 20423
presented at, pp. 16-23.
12. Kashirina, K.O.; Telkov, A.P. (2010). A brief analysis of some
analytical solutions of the problems about fluid flow to the vertical crack of hydraulic fracturing. Oil-field Engineering 9, pp. p. 9-13.
13. Mirzajanzade, A., & Gevinyan, G. (1977). Hydraulics of Clay and
Cement Solutions, Moscow: Nedra, p.229.
Follow us !











